My research focuses on cosmology and large-scale structure evolution and formation.
Research

Cosmic Emulator
To obtain precise cosmological parameter constraints, we need to know the accurate prediction for the statistics in every cosmological model, and then run the MCMC process on the measured statistics from observations. For previous surveys, we use the theoretical preditions such as halo model. While for DESI, CSST and after, we need more accurate predicitons. Running simulations is the ultimate way. But due to the limited computational resources, we can only sample the whole (6D~8D) cosmological parameter space using O(100) simulations. We complete this sampling by Sobol sequence, and ran 129 simulations, each with particle number about 30 billion. This high resolution cosmological simulation suite is named as Kun, upon which the CSST Emulator is constructed for China Space Station Survey Telescope (CSST) cosmology science. The emulator for various statistics including those non-Gaussian ones containing information beyond two point, is under designing.
- Kun Universe [readthedocs]
- CSST Emulator [GitHub]
- CSST Cosmological Emulator I: Matter Power Spectrum Emulation with one percent accuracy to k=10 h/Mpc [ArXiV], [ADS]
- CSST Cosmological Emulator II: Generalized Accurate Halo Mass Function Emulation [ArXiV], [ADS], [doi]
- CSST Cosmological Emulator III: Hybrid Lagrangian Bias Expansion Emulation of Galaxy Clustering [ArXiv], [SCPMA]

Nonlinear Reconstruction
Given a nonlinear density map, one can find a distorted mesh on which the density is constant. This mesh provides an estimation of the displacement field. One can obtain the density field in Lagrangian space, i.e. the divergence of the displacement, which is referred as the reconstructed density field. This reconstructed density field has much better cross-correlation with the initial condition and thus sharpened baryon acoustic oscillation peaks. When working in redshift-space, it also makes the redshift-space distortion signal more linear, providing more stringent constraints on the growth rate of our Universe.
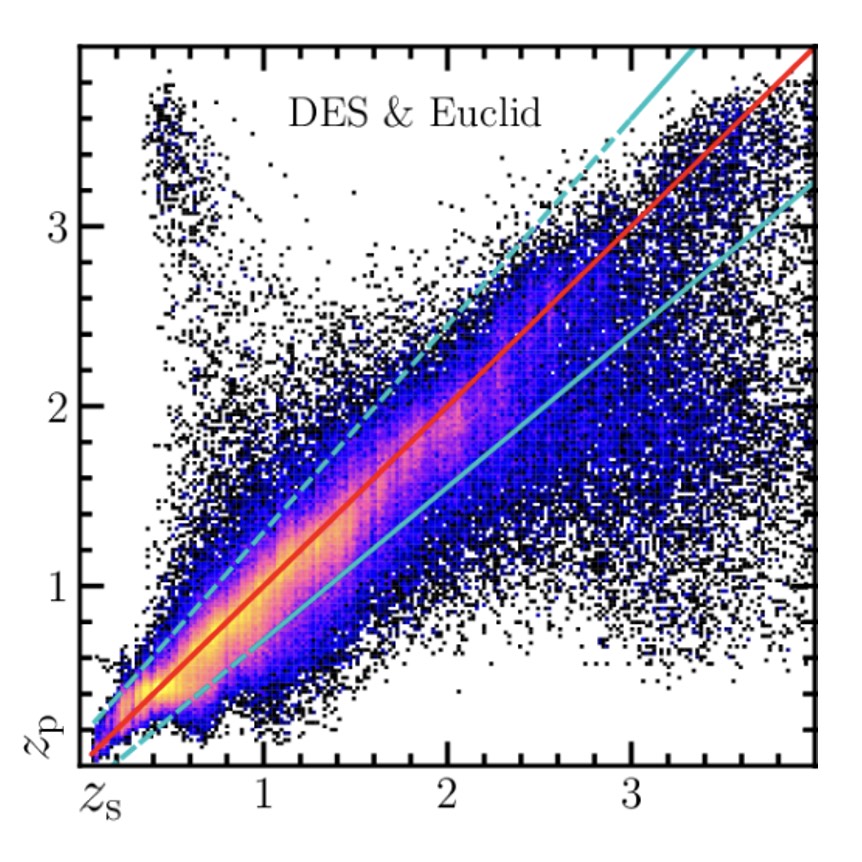
Redshift Calibration
Imaging surveys provide photometric redshifts for the galaxies, obtained from the photometry measure and the follow-up photo-z pipeline. Photo-z is typically with an uncertainty about 0.05(1+z) for Stage-III surveys. This uncertainty is one of the major systematics in weak lensing cosmology. Self-calibration method utilizes the cross correlations measured between different redshift bins to solve out the redshift distribution, with less assumptions and with no need of the external spectroscopic redshift dataset. With the recent development after 2020, it can provide the redshift distribution on fine bins (dz~0.05) and is applicable on real observations (such as DeCALS and DES). The performance is comparable to the independent cross-calibration methods.
- Self-calibration Algorithm [GitHub]
- Self-calibration of photometric redshift scatter from DECaLS DR8 power spectrum and validation with simulated catalogues [ArXiV], [ADS]
- Using angular two-point correlations to self-calibrate the photometric redshift distributions of DECaLS DR9 [ArXiV], [ADS]
- Precise self-calibration of interloper bias in spectroscopic surveys [ArXiV], [ADS]
- Reconstructing redshift distributions with photometric galaxy clustering [ArXiV], [ADS]
- Redshift Distributions of Fast Radio Bursts Inferred Using Clustering in Dispersion Measure Space [ArXiv], [ADS]
Lensing signal hidden in galaxy distribution
Weak lensing signal can be measured by looking at a large number of galaxy shapes, since the galaxy shapes are slightly changed by the weak lensing field, so-called cosmic shear. Weak lensing also changes the galaxy flux/size, and (de)magnifies the sky portions, leading to a change of the galaxy number density, so-called cosmic magnification.
Extracting the lensing signal from the galaxy distribution is very challenge, due to the intrinsic clustering signal which is several orders of magnitude larger. In future observation, the dependence of the cosmic magnification on the galaxy luminosity function can be measured precisely. Taking use of this dependence, one can separate cosmic magnification signal from the intrinsic clustering.
- Weak lensing reconstruction through cosmic magnification - II. Improved power spectrum determination and map-making [ArXiV], [ADS]
- Weak-lensing Power Spectrum Reconstruction by Counting Galaxies. I. The ABS Method [ArXiV], [ADS]
- Weak-lensing Power Spectrum Reconstruction by Counting Galaxies. II. Improving the ABS Method with the Shift Parameter [ArXiV], [ADS]
- Weak Lensing Magnification Reconstruction with the Modified Internal Linear Combination Method [ArXiV], [ADS]
- A method of weak lensing reconstruction through cosmic magnification with multi-band photometry information [ArXiV], [ADS]
- Attempt to reconstruct weak lensing by counting DECaLS galaxies [ArXiV], [ADS]
- Weak Lensing Reconstruction by Counting Galaxies: Improvement with DES Y3 Galaxies [ArXiV]
- Meta-Calibration of the Cosmic Magnification Coefficient: Toward Unbiased Weak Lensing Reconstruction by Counting Galaxies [ArXiv]
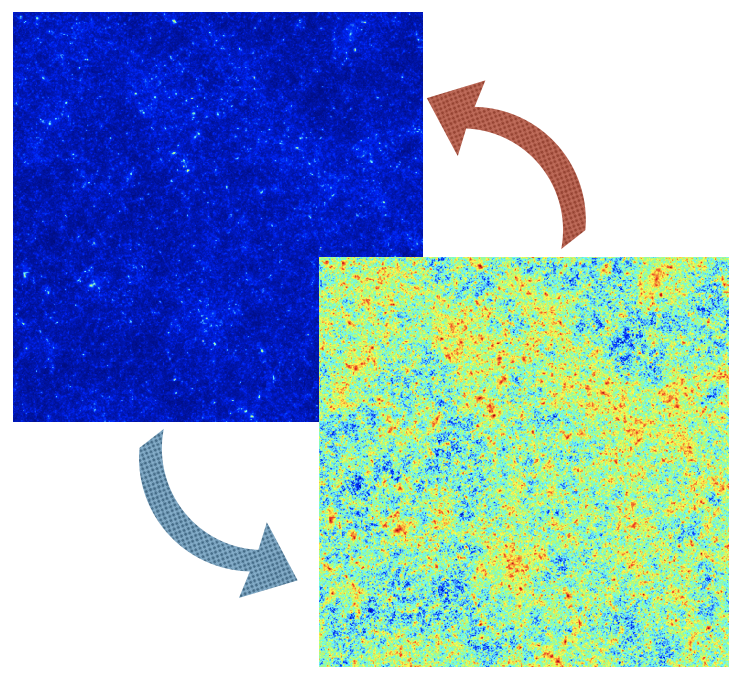
The non-Gaussianity of the lensing field
After a logarithmic transform, the matter density field is Gaussianized. This process changes the information hierarchy structure, and the amount of information in power spectrum is increased.
Weak lensing field shares the similar property. In the first work we proved that the weak lensing field could be effectively Gaussianized by a local transform. However, the severe shape noise (the intrinsic shape of galaxies) hampers the application of the local transform. In the second work, wiener filtering is proposed to overcome this problem and recover the ability of the local transform.
Based on the finding that weak lensing field can be effectively Gaussianized by a local transform, we proposed the inverse-Gaussianization method to fast generate large amount of lensing mocks. These mocks have correct power spectrum and reasonably good power spectrum covariance. We also find that the peak height counts and peak steepness counts are well produced. In the covariance of peak statistics, super sample variance is a key ingredient and we also extend the inverse-Gaussianization method to include the super sample variance.
- Gaussianizing the non-Gaussian lensing convergence field: The performance of the Gaussianization [ArXiV], [ADS]
- Gaussianizing the non-Gaussian lensing convergence field II. The applicability to noisy data [ArXiV], [ADS]
- Fast generation of weak lensing maps by the inverse-Gaussianization method [ArXiV], [ADS]
- Weak-lensing Peak Statistics in Mocks by the inverse-Gaussianization method [ArXiV], [ADS]

The non-Gaussianity of the matter field
Due to the late-time nonlinear evolution of the Universe, the cosmic fields are non-Gaussian. The information is transferred into high-order statistics, which is complicated and hard to model and measure. However, the local transform is found to be effective to Gaussianize the fields and pull the information back to power spectrum. But the local transform is imperfect. We can find some residual non-Gaussianity in the small scale. The perfectness of the local transform methods rely on the Gaussian Copula Hypothesis. We revisit this Hypothesis 10 years after it was proposed first time. Using high resolution simulation, we find obvious deviation from Gaussian copula in its differential form.
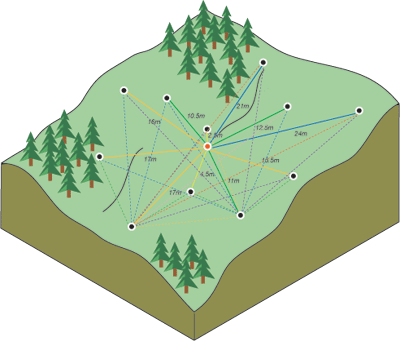
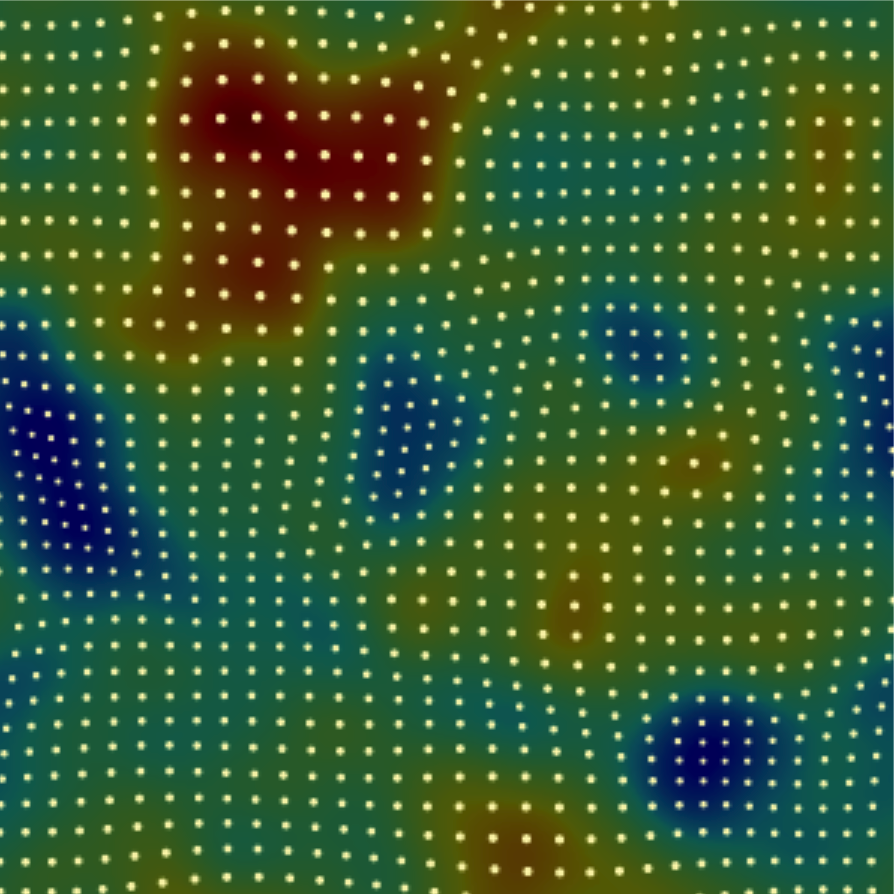
Kriging interpolating cosmic velocity field
Volume-weighted statistics of large-scale peculiar velocity is preferred by peculiar velocity cosmology, since it is free of the uncertainties of galaxy density bias entangled in observed number density-weighted statistics. However, measuring the volume-weighted velocity statistics from galaxy (halo/simulation particle) velocity data is challenging.
In this series of works, we attempt to obtain volume-weighted velocity power spectrum by isotropic Kriging, an interpolation method widely used in geoscience. Kriging provides the most likely velocity field based on the data around and the prior correlation function.