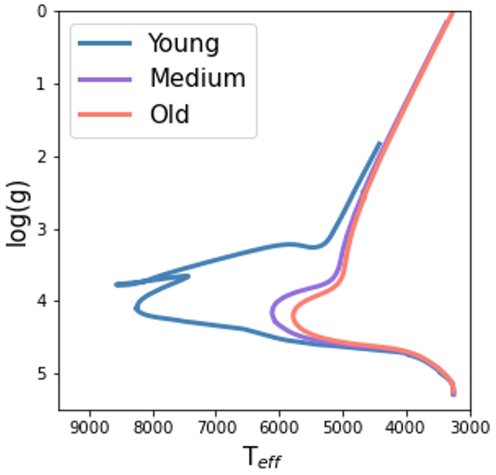
银盘恒星按其化学丰度、空间分布及运动学特征,一般可以分为薄盘与厚盘两个成分。薄盘星较为年轻,金属丰度高,垂直方向上集中分布在银盘中平面附近;厚盘星则更为年老,金属丰度较低,在垂直方向分布较为弥散。这些性质上的巨大差异表明厚盘与薄盘有着不同的起源及演化过程,厚盘很可能形成于银河系演化的早期,后续与卫星星系的并合及盘内的各种动力学过程使其在垂向显著增厚;而薄盘恒星则由聚集在银河系盘面的冷气体持续形成。
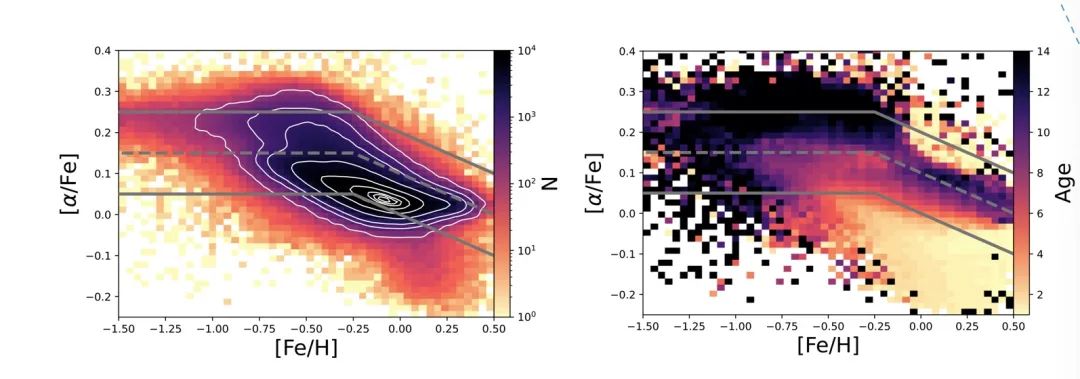
图2显示样本在化学丰度参数空间([α/Fe]—[Fe/H])的分布。左图显示了数密度分布,虚线标记了薄盘(虚线下部)与厚盘(虚线上部)的大致区分。右图利用恒星平均年龄进行了颜色标记,可见薄盘星整体上相比于厚盘星更加年轻,符合对这两类恒星的理论预期。因为恒星绕银心的运动轨道并不是纯圆周运动,为了消除恒星的径向运动对其所处的轨道半径的影响,他们采用了恒星引导中心半径(Rg,其示踪轨道角动量)来重构金属丰度径向梯度,该方法不受恒星当前所在位置的影响,能够反映出更加本征的金属丰度径向梯度。
研究人员综合了化学丰度与恒星轨道在垂直于银盘方向的最高位置(Zmax)选择了薄盘星([α/Fe]较低,Zmax较小)与厚盘星样本([α/Fe]较高,Zmax较大),并分别研究了其中不同年龄的星族体现出的金属丰度径向梯度。图3显示了金属丰度径向梯度随恒星年龄的变化,可见薄盘星(左图)的金属丰度径向梯度随年龄增长愈发平缓,最年轻的恒星则显示出了最陡的金属丰度径向梯度。他们发现的金属丰度梯度随恒星年龄增长逐渐趋于平坦,这一现象与经典理论预期的结果(即年老恒星金属丰度梯度更陡,年轻恒星金属丰度梯度平缓)相反。这一结果可能是存在显著径向迁移效应的重要观测证据:由于年老的恒星在一生中有更大的概率与银河系的旋臂相互作用而发生径向迁移现象,因此相比于年轻恒星,其金属丰度的梯度可以被逐渐抹平。
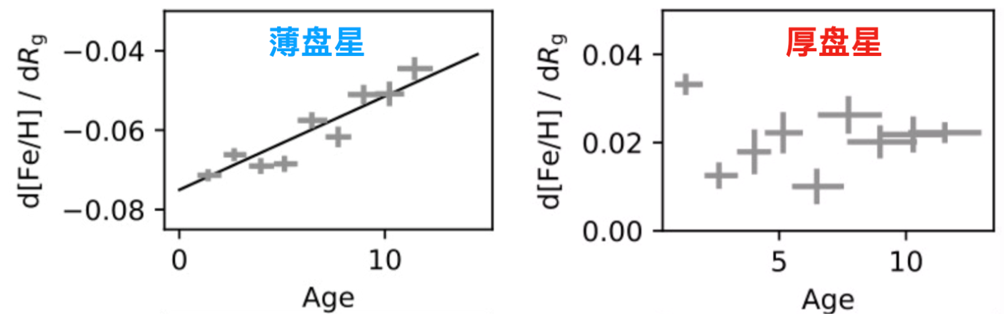
图3薄盘星(左图)与厚盘星(右图)的金属丰度径向梯度随年龄的变化
但是,更古老的厚盘却很不一样:厚盘星的金属丰度显现微弱的内低外高的正梯度(如图3右图所示)。厚盘与年轻的薄盘有不同的形成机制和演化过程,但两种盘结构互相耦合在一起。他们利用恒星示踪金属丰度梯度的方法,便可分别反映出这两种盘结构不同的演化过程。与一些河外星系的厚盘观测结果类似,银河系厚盘不同星族体现出正的金属丰度梯度,这很可能是由于银盘内区早期大量吸积了极低金属丰度的气体,造成了外围金属丰度高于内区的现象。为了确定结果的可靠性,他们也测试了不同的薄盘与厚盘选择条件,发现他们的结果并不受这些不同选择判据的影响。这确认了他们重构出的薄盘与厚盘金属丰度梯度随年龄的变化是可靠的,也说明薄盘与厚盘的确经历了不同的化学增丰及动力学演化过程。
论文的通讯作者之一沈俊太教授指出:“我们发现薄盘中年轻恒星的金属丰度梯度很陡,显著高于年老恒星的结果,这说明恒星的径向迁移可能在整个银盘的形成演化历史中起到了非常重要的作用。我们的研究对这一现象给出了直接的观测证据,有助于揭示出银河系结构形成及动力学演化历史”。
论文第一作者为课题组博士后John Vickers,沈俊太教授与李兆聿副教授为共同通讯作者。研究团队得到了国家自然科学基金、国家重点研发基金、教育部111计划以及上海市自然科学基金的资助;本工作的数据处理使用了上海交通大学天文系Gravity集群。
相关论文链接:
"The Flattening Metallicity Gradient in the Milky Way's Thin Disk", Vickers; Shen; Li, 2021, ApJ, 922,189
(https://iopscience.iop.org/article/10.3847/1538-4357/ac27a9)